El índice de trabajo WI, es un parámetro que depende del material y del equipo de conminución, por lo que es conveniente que en su obtención se utilice un mecanismo de ruptura similar al de la máquina para la cual se efectúa la determinación. Así, por ejemplo, se puede hacer ensayos de impacto (simulando etapas de trituración del material), ensayos en molinos de barras y ensayos en molinos de bolas, según se describe a continuación.
Test estándar de chancabilidad
El procedimiento experimental estándar de laboratorio, para determinar el índice de trabajo en la etapa de chancado, básicamente consiste en lo siguiente:
- Preparar el material a un tamaño comprendido entre 2 y 3 pulgadas.
- Colocar parte de dicho material entre 2 péndulos opuestos e iguales (30 lbs de peso cada uno), que pueden levantarse controladamente a distintas alturas de caída.
- Efectuar un test de impacto sobre el material, colocando la dimensión menor de la roca en la dirección del impacto a producir por ambos péndulos, los cuales se levantarán progresivamente, hasta producir la fractura requerida del material.
- El índice de trabajo (W¡; kwh/ton. corta) se calculará de un promedio de 10 test exitosos, mediante la fórmula:
- Preparar el material a un tamaño comprendido entre 2 y 3 pulgadas.
- Colocar parte de dicho material entre 2 péndulos opuestos e iguales (30 lbs de peso cada uno), que pueden levantarse controladamente a distintas alturas de caída.
- Efectuar un test de impacto sobre el material, colocando la dimensión menor de la roca en la dirección del impacto a producir por ambos péndulos, los cuales se levantarán progresivamente, hasta producir la fractura requerida del material.
- El índice de trabajo (W¡; kwh/ton. corta) se calculará de un promedio de 10 test exitosos, mediante la fórmula:
Donde:
W¡ = índice de trabajo del material, aplicable a chancado (kwh/ton corta)
Ds = gravedad especifica del sólido
C = esfuerzo del impacto aplicado, necesario para fracturar el material (lb-pie/pulg de espesor de la roca).
W¡ = índice de trabajo del material, aplicable a chancado (kwh/ton corta)
Ds = gravedad especifica del sólido
C = esfuerzo del impacto aplicado, necesario para fracturar el material (lb-pie/pulg de espesor de la roca).
Test estándar de Moliendabilidad para Molinos de barras
El índice de trabajo del material, aplicable a la molienda gruesa en molinos de barras, se determina en un molino estándar de laboratorio de 12 pulgadas de diámetro y 24 pulgadas de largo, conteniendo:
- 6 barras de 1 I/4 pulg. de diámetro x 21 pulg. de largo
- 2 barras de 1 3/4 pulg. de diámetro x 21 pulg. de largo
cuyo peso total es de 33.380 gramos.
La alimentación al molino corresponde a material triturado controladamente a 100% - 1/2", ocupando un volumen aparente, de 1250 cm3 dentro de un recipiente cilíndrico apropiado. Este material se pesa, se tamiza (análisis granulométrico de la muestra de alimentación) y se muele en seco en el molino de barras (que dispone de revestimiento tipo ondulatorio, de un contador de revoluciones y gira a una velocidad constante de rotación de 46 RPM), simulando una operación en circuito cerrado con 100% de carga circulante (usando mallas de corte entre 4 y 65 mesh, para simular la etapa de clasificación del circuito cerrado de molienda operando bajo diferentes tamaños de corte).
A objeto de equiparar la segregación del material en ambos bordes del molino, se hará girar éste en su posición horizontal normal por ocho revoluciones, inclinándolo entonces 5° hacia arriba y girándolo por una revolución, 5° hacia abajo (dándole otra revolución), devolviéndole entonces su posición horizontal normal, para hacerlo girar durante ocho revoluciones adicionales. Este procedimiento se repetirá en forma continua durante cada ciclo de molienda.
Los test de molienda se efectuarán en seco, variando la malla de corte entre 4 y 65 mallas Tyler. Al final de cada periodo (ciclo) de molienda, se descargará el molino inclinándolo 45° hacia abajo haciéndolo rotar durante 30 revoluciones, tamizando entonces el producto de molienda en el harnero seleccionado como malla de corte del circuito. Se pesará el bajo tamaño del harnero (undersize), dejándolo aparte, y se agregará una porción equivalente de alimentación fresca no segregada al sobre tamaño del harnero (oversize), a objeto de reconstituir la carga inicial de sólidos alimentada al molino en cada ciclo (completando el volumen aparente de 1.250 cm3 de material, en cada período de molienda). Todo este material será
entonces retomado al molino, moliéndolo durante un tiempo equivalente al número de revoluciones calculado para dar una carga circulante igual al peso de alimentación fresca agregada (o sea, un 100% de carga circulante). Los ciclos de molienda continuarán entonces, hasta que los gramos netos de undersize producidos por revolución alcancen el equilibrio; invirtiéndose comúnmente la dirección de crecimiento o disminución del índice de moliendabilidad (g/rev) calculado durante los tres últimos ciclos. Una vez alcanzado el equilibrio, se analizará en detalle la distribución granulométrica del undersize del harnero (producto final del circuito de molienda), a objeto de calcular el tamaño 80% pasante de dicho producto (P80;microgramos) y se calculará el índice de moliendabilidad en molino de barras (Grp; g/rev), promediando los tres últimos valores de gramos netos de undersize producidos por revolución del molino. El 'índice de trabajo del material, válido para molienda en molinos de barras, se calculará según la expresión:

Donde:
P100 : abertura en micrones de la malla de corte utilizada para cerrar el circuito (tamaño 100% pasante del producto)
Grp : gramos de undersize (producto final del circuito) producido por revolución del molino de barras, bajo condiciones de equilibrio (100% carga circulante)
F80 : tamaño 80% pasante de la alimentación fresca al circuito de molienda (micrómetros)
P80 : tamaño 80% pasante del producto final del circuito de molienda (micrómetros)
WI : índice de trabajo del material (kwh/ton corta)
El valor del índice de trabajo calculado según la expresión anterior, es consistente con la potencia mecánica de salida de un motor capaz de accionar un molino de barras del tipo descarga por rebalse de 8 pies de diámetro interno (medido entre revestimientos), moliendo en húmedo y en circuito abierto. Para el caso de molienda en seco, el consumo de energía base deberá ser multiplicado por 1,30. Como la eficiencia en la molienda varia según el diámetro interno del molino (D; pies), el consumo base de energía deberá ser multiplicado por el factor (8/D)^0,2 considerando un valor de 0,9146 como cota inferior de dicho factor para D mayor o igual a 12, 5pies. Bond propone además utilizar factores correctores específicos para los supuestos casos en que se tenga una alimentación demasiado gruesa, una baja o alta razón de reducción en el molino y otra corrección aplicable al grado de uniformidad del material alimentado al molino.
Test Standard de Moliendabilidad para Molinos de Bolas
El índice de trabajo del material, aplicable a la molienda fina en molinos de bolas, se determina en un molino estándar de laboratorio de 12" diámetro x 12 largo, que gira a 70 RPM posee esquinas redondeadas y revestimiento liso (exceptuando la puerta de carga del material; de 4” x 8"), conteniendo además la siguiente carga balanceada de bolas de acero:
Diámetro de bola (pulgada)
| n° aproximado de bolas | Peso bolas (g) | Área superficial (Pulg2) |
| 1.45 | 43 | 8.803 | 285 |
| 1.17 | 67 | 7.206 | 289 |
| 1.00 | 10 | 0.672 | 32 |
| 0.75 | 71 | 2.011 | 126 |
| 0.61 | 94 | 1.433 | 110 |
| Total | 285 | 20.125 | 842 |
Cuyo peso total es de 20.125 gramos.
La alimentación al molino corresponde a material triturado controladamente a 100% - 6 mallas Tyler (pudiendo utilizarse una alimentación más fina en caso necesario); con un volumen aparente de 700 cm3 (medido en una probeta cilíndrica graduada). Este material se pesa, se tamiza (análisis granulométrico de la muestra de alimentación) y se muele en seco en un molino de bolas (que cuenta además con un contador de revoluciones), simulando entonces una operación en circuito cerrado con 250% de carga circulante (utilizando la malla de corte requerida) para cerrar el circuito se podrá utilizar tamices entre 28 y 325 mallas Tyler, dependiendo del tamaño de corte que se quiera simular.
El test de Bond se inicia moliendo el material por 100 revoluciones, se vacía el molino con la carga de bolas, y se tamizan los 700 cm3 de material sobre el harnero seleccionado como malla dc corte del circuito (usando mallas protectoras mas gruesas, en caso necesario). Se pesa el bajo tamaño del harnero (undersize), dejándolo aparte; agregando carga fresca no segregada al sobretamaño del harnero (oversize) para reconstituir la carga inicial de sólidos alimentada al molino en cada ciclo (se completa el volumen aparente a 700 cm3 de carga al molino) Todo este material se retoma al molino, junto con la carga de bolas. siendo dicho material molido por el número de revoluciones calculado para producir un 250% de carga circulante.
El índice de trabajo del material, válido para molienda en molinos de bolas. se calculará (según la siguiente expresión empírica desarrollada por Bond para materiales heterogéneos:
Donde :
WI : índice de trabajo del material (kwh/ton corta)El valor del índice de trabajo calculado según la expresión anterior es consistente con la potencia mecánica de salida de un motor capaz de accionar un molino de bolas del tipo descarga por rebalse, de 8 pies de diámetro interno (medido entre revestimientos). moliendo en húmedo y en circuito cerrado con un clasificador. Para el caso de molienda en seco, el consumo base de energía se deberá multiplicar normalmente por un factor 1.30. Como la eficiencia en la molienda varía según el diámetro interno del molino (D: pies), se deberá multiplicar el consumo base de energía por el factor (8D)0,2. considerando no obstante un valor mínimo de 0.9146 para dicho factor, en el supuesto caso que D mayor o igual a 12,5 pies. Fred Bond propone utilizar además otros factores correctores aplicables a los casos de molienda en circuito abierto, alimentación demasiado gruesa, sobremolienda excesiva de finos y baja razón de reducción en el molino. Bond también señala que en aquellos casos en que el valor de P80 no puede ser determinado experimentalmente, se podrán adoptar los siguientes valores promedios, como primera aproximación:
P100 : abertura en micrones de la malla de corte utilizada para cerrar el circuito (tarnaño 100% pasante del producto)
Gbp : índice de moliendabilidad del material en molinos de bolas (g/rev.)
F80 : tamaño 80% pasante de la alimentación fresca al circuito (micrómetros).
P80 : tamaño 80% pasante del producto final del circuito (micrómetros).
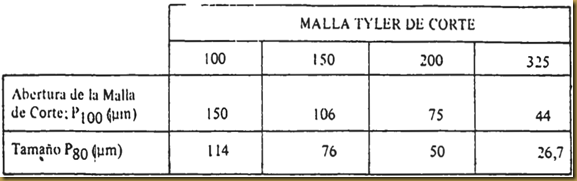
obsérvese de la tabla anterior que la relación aproximada entre P80 (micrómetros) y P100 (micrómetros) es como sigue:

Una ecuación simplificada propuesta anteriormente por Bond para materiales homogéneos y que, según algunos investigadores. proporciona mejores resultados, es la siguiente:
Tercer Principio: La falla más débil del material determina el esfuerzo de ruptura, pero la energía total consumida está controlada por la distribución de fallas en todo el rango de tamaños involucrado, correspondiendo al promedio de ellas.
Aún cuando Bond extrajo parte de sus ideas de trabajos de investigación desarrollados en el área de fractura de sólidos, tales como el de Griffith en 1920, su análisis relativo a la conminución debe ser considerado como de carácter netamente empírico. El objetivo de los trabajos desarrollados por Bond fue llegar a establecer una metodología confiable para dimensionar equipos y circuitos de conminución, y en este sentido, el método de Bond ha dominado el campo por casi 25 años. Solamente en la última década, han aparecido métodos alternativos que prometen desplazar definitivamente el procedimiento estándar de Bond, situación que todavía no se ha concretado en forma generalizada. En realidad, el método de Bond proporciona una primera estimación (error promedio de ± 20%) del consumo real de energía necesario para triturar y/o moler un material determinado en un equipo de conminución a escala industrial. No obstante y debido a su extrema simplicidad, el procedimiento
estándar de Bond continúa aún siendo utilizado en la industria minera para dimensionar chancadoras, molinos de barras y bolas a escalas piloto, semi industrial e industrial.
De acuerdo a los resultados de innumerables pruebas estándar de Bond a escala de laboratorio, el índice de trabajo promedio para cobres porfídicos es del orden de 12,73 kwh/ton corta, mientras que para menas porfídicas de molibdeno es de 12,80; confirmando así la gran similitud en tipos de rocas de estos minerales. Contrario a esto, la roca andesitica dura presenta un índice de trabajo de 18,253 la roca dior1'tica.de 20,90; granito, 15,13; y los minerales blandos tales como bauxita, de 8,78; barita, 4,73; arcillas, 6,30; y fosfatos, 9,92.
Métodos Indirectos de Determinación del Índice de Trabajo (W¡).
El índice de trabajo para un material en particular se determina en el laboratorio mediante el respectivo test estándar de chancabilidad o moliendabilidad (molinos .de barras y bolas) descrito por Bond, quien desarrolló una metodología separada para cada situación en particular. Los métodos simplificados descritos en esta sección para calcular el índice de trabajo de un material en molinos de bolas,proporcionan una aproximación razonable del respectivo valor obtenido en el test estándar de Bond. siendo apropiado su uso en aquellos casos en que no exista ya sea el equipo estándar disponible, la cantidad total de material requerida en dicho test estándar. o bien, cuando no se dispone del tiempo o personal apropiado para ejecutar dicho test, sirviendo muchas veces un valor aproximado de Wi como mera referencia.
Existen ciertas dificultades e inconvenientes al utilizar el método estándar de Bond para determinar el índice de moliendabilidad Wi de una muestra. Una de ellas es la necesidad de disponer de un molino de bolas tipo Bond, el cual puede no estar inmediatamente disponible en el laboratorio, especialmente cuando este último se encuentra ubicado en la propia Planta. Otra desventaja es el requerimiento de aproximadamente 10 kg de muestra de alimentación, la que necesita de una preparación especial. Finalmente, la ejecución del test consume bastante tiempo, ya que un solo test estándar de Bond requiere de un día completo de trabajo (8 horas) de un técnico especializado.
Cuando el índice de trabajo de un material deba emplearse para dimensionar un circuito industrial de molienda. es evidente la necesidad de obtener la mejor estimación posible de dicho valor, lo cual requerirá necesariamente de la ejecución completa de uno (o más) test(s) estándar de Bond. Sin embargo, si los datos de moliendabilidad de un material son utilizados solamente con fines de control metalúrgico de la operación, será factible sacrificar un poco de precisión, a cambio de la significativa cantidad de tiempo que se ganará a través de un método de cálculo más simplificado. En el pasado, se han realizado algunos intentos para determinar el índice de trabajo de Bond mediante diversas técnicas simplificadas, las que se revisan brevemente a continuación.
Existen ciertas dificultades e inconvenientes al utilizar el método estándar de Bond para determinar el índice de moliendabilidad Wi de una muestra. Una de ellas es la necesidad de disponer de un molino de bolas tipo Bond, el cual puede no estar inmediatamente disponible en el laboratorio, especialmente cuando este último se encuentra ubicado en la propia Planta. Otra desventaja es el requerimiento de aproximadamente 10 kg de muestra de alimentación, la que necesita de una preparación especial. Finalmente, la ejecución del test consume bastante tiempo, ya que un solo test estándar de Bond requiere de un día completo de trabajo (8 horas) de un técnico especializado.
Cuando el índice de trabajo de un material deba emplearse para dimensionar un circuito industrial de molienda. es evidente la necesidad de obtener la mejor estimación posible de dicho valor, lo cual requerirá necesariamente de la ejecución completa de uno (o más) test(s) estándar de Bond. Sin embargo, si los datos de moliendabilidad de un material son utilizados solamente con fines de control metalúrgico de la operación, será factible sacrificar un poco de precisión, a cambio de la significativa cantidad de tiempo que se ganará a través de un método de cálculo más simplificado. En el pasado, se han realizado algunos intentos para determinar el índice de trabajo de Bond mediante diversas técnicas simplificadas, las que se revisan brevemente a continuación.
Método de Berry y Bruce
En 1966, los investigadores Berry y Bruce desarrollaron un método indirecto de laboratorio para estimar el índice de Bond en molinos de bolas, comparando las respectivas distribuciones granulométricas de alimentación fresca y producto final de dos muestras distintas (muestra de referencia y muestra test), molidas bajo idénticas condiciones operacionales en un molino estándar de laboratorio. La muestra de referencia corresponde aun material cualquiera seleccionado, cuyo Wi es conocido; mientras que la muestra test corresponde a aquella cuyo Wi se requiere estimar (i.e.; con un valor desconocido de Wi). El equipo utilizado por los autores corresponde a un molino estándar Paul-Abbe de 12 pulgadas de diámetro interno, y la alimentación se prepara en forma controlada a una granulometría de 100% -10 mallas Tyler (no obstante lo anterior, el tamaño del molino, carga de bolas, etc., no son restrictivos en la práctica, pudiendo utilizarse otras condiciones operacionales estándar previamente definidas por el usuario para tales efectos). El procedimiento experimental sugerido por los autores es como sigue:
En 1966, los investigadores Berry y Bruce desarrollaron un método indirecto de laboratorio para estimar el índice de Bond en molinos de bolas, comparando las respectivas distribuciones granulométricas de alimentación fresca y producto final de dos muestras distintas (muestra de referencia y muestra test), molidas bajo idénticas condiciones operacionales en un molino estándar de laboratorio. La muestra de referencia corresponde aun material cualquiera seleccionado, cuyo Wi es conocido; mientras que la muestra test corresponde a aquella cuyo Wi se requiere estimar (i.e.; con un valor desconocido de Wi). El equipo utilizado por los autores corresponde a un molino estándar Paul-Abbe de 12 pulgadas de diámetro interno, y la alimentación se prepara en forma controlada a una granulometría de 100% -10 mallas Tyler (no obstante lo anterior, el tamaño del molino, carga de bolas, etc., no son restrictivos en la práctica, pudiendo utilizarse otras condiciones operacionales estándar previamente definidas por el usuario para tales efectos). El procedimiento experimental sugerido por los autores es como sigue:
Se molerán 2000 gramos de la muestra test (con Wi desconocido) en el molino de bolas estándar, bajo condiciones de molienda húmeda, por un período de tiempo suficiente ( para alcanzar el grado de fineza deseado en el producto Final(ejemplo: x %- 200 #, u otro valor de referencia). La misma cantidad de muestra de referencia (cuyo Wi se conoce a priori) se molerá por el mismo tiempo de molienda y bajo condiciones operacionales idénticas a las de la muestra test, Se analizarán granulométricamente la alimentación y descarga del molino en ambos casos (muestra test y muestra de referencia), a objeto de determinar los respectivos valores de F80 y P80.
Como el test de molienda se efectúa con cantidades idénticas de material sólido en ambos casos y bajo las mismas condiciones operacionales (% de sólidos, carga de bolas, RPM del molino, tiempo de molienda. etc.), la cantidad de energía consumida al moler la muestra ( test será aproximadamente igual a aquella utilizada en moler la muestra de referencia. Así,
utilizando la expresión general de Bond, podremos escribir la siguiente relación:
 Los subíndices t y r se refieren a la muestra test y muestra de referencia, respectivamente.
Los subíndices t y r se refieren a la muestra test y muestra de referencia, respectivamente.La ecuación ultima permite estimar el índice de trabajo de la muestra test en función del índice de trabajo de la muestra de referencia.
El método en sí es bastante simple, rápido de llevar a cabo y requiere de un molino de bolas convencional de laboratorio, el cual generalmente se puede adaptar convenientemente para la ejecución del test. Todo lo que se requiere es un stock apropiado de muestra de referencia. cuyo índice de trabajo haya sido previamente determinado en un molino estándar de Bond. La principal restricción del método se encuentra en su nivel de precisión, ya que la eficiencia de molienda normalmente varía con las características físicas y reológicas de la pulpa en el molino. las que en gran medida son afectadas por la proporción de finos presente en la alimentación y por el porcentaje de sólidos de la pulpa alimentada al molino. Aun cuando el % de sólidos se mantenga constante para ambas muestras (test y de referencia), la distribución granulométrica inicial de dichas muestras debería ser idéntica a objeto de garantizar la validez de la ultima ecuación arriba, en todos los casos. Así, el hecho de mantener constante la carga de sólidos en el molino, el mismo input de energía en la molienda y las mismas condiciones operacionales durante la ejecución del test con ambos tipos de muestras, no garantiza siempre la validez teórica y/o práctica de la ecuación (2.41) en todos los casos, a menos que se satisfaga la condición adicional de utilizar la misma distribución granulométrica inicial en la muestra test y la de referencia.
No obstante las limitaciones mencionadas, y considerando la necesidad práctica de determinar el índice de trabajo de muestras de concentrados, relaves y otros productos intermedios de circuitos de flotación, a objeto de dimensionar las correspondientes unidades industriales (tales como molinos de remolienda y otros), la empresa INCO Metals of Canada
(J. Roy Gordon Research Laboratory) introdujo en 1975 una leve variación a la metodología originalmente propuesta por Berry & Bruce en 1966. la cual demostró ser bastante efectiva en la mayor parte de los casos analizados, según se discute brevemente a continuación.
Tal como se señalara anteriormente. la mayor restricción del método de Berry & Bruce consiste en la imposibilidad física de comenzar el test con la misma distribución granulométrica inicial en la muestra test y la muestra de referencia (esto es particularmente critico cuando se desea por ejemplo determinar el Wi de un concentrado de cobre cuya granulometría inicial es de = 100% - 65 mallas, lo que viola de inmediato la primera condición del test estándar de Bond en molinos de bolas (P100=6#Tyler; disponiéndose por lo general de un material de referencia con granulometría mas gruesa, del orden de 100% - 6 # Tyler). Para obviar este problema y, considerando además que los tamaños característicos que realmente influyen en el cálculo de Wi (según Bond) son los valores de F80 (micrómetros) y P80 (micrómetros), se recomienda utilizar la siguiente metodología, que ha demostrado ser bastante efectiva en la determinación indirecta de índices de trabajo para una gran variedad de materiales
(J. Roy Gordon Research Laboratory) introdujo en 1975 una leve variación a la metodología originalmente propuesta por Berry & Bruce en 1966. la cual demostró ser bastante efectiva en la mayor parte de los casos analizados, según se discute brevemente a continuación.
Tal como se señalara anteriormente. la mayor restricción del método de Berry & Bruce consiste en la imposibilidad física de comenzar el test con la misma distribución granulométrica inicial en la muestra test y la muestra de referencia (esto es particularmente critico cuando se desea por ejemplo determinar el Wi de un concentrado de cobre cuya granulometría inicial es de = 100% - 65 mallas, lo que viola de inmediato la primera condición del test estándar de Bond en molinos de bolas (P100=6#Tyler; disponiéndose por lo general de un material de referencia con granulometría mas gruesa, del orden de 100% - 6 # Tyler). Para obviar este problema y, considerando además que los tamaños característicos que realmente influyen en el cálculo de Wi (según Bond) son los valores de F80 (micrómetros) y P80 (micrómetros), se recomienda utilizar la siguiente metodología, que ha demostrado ser bastante efectiva en la determinación indirecta de índices de trabajo para una gran variedad de materiales
- Determinación del Work Index del Material de Referencia (Wir): Primeramente, se determinará el índice de trabajo del material de referencia (Wir), empleando la metodología y equipo estándar de laboratorio propuestos por Bond. Para ello, se seleccionará a priori el tamaño de corte (P100) que se requiere obtener en el circuito industrial con la muestra test, efectuando entonces el correspondiente test estándar de moliendabilidad sobre la muestra de referencia. A modo de ejemplo, si la muestra test corresponde a un concentrado primario de cobre cuya granulometría inicial es de 100% - 65 mallas, y si se requiere remoler esta muestra a una
granulometría final de 90% – 325#, convendrá seleccionar una malla Tyler 270 como tamaño de corte (P100 :53 micrómetros), para la ejecución del test estándar de Bond sobre la muestra de referencia (que podría ser, por ejemplo, un mineral de cobre con granulometría de 100% - 6 # Tyler. A objeto de mejorar la eficiencia del tamizaje, se podría efectuar dicho tamizado en húmedo, aun cuando el Test estándar de Bond deba realizarse en seco. Previamente, se prepararán unos 20 kg de material de referencia a 100% - 6 # Tyler (mediante trituración controlada), efectuándose un análisis granulométrico completo de la alimentación fresca al molino de Bond (a objeto de calcular el valor de F80 (micrómetros) y el % de bajotamaño presente en dicha muestra). Una vez completado el test estándar de Bond, se determinarán los valores de Gbp (g/rev.) y tamaño P80 (micrómetros) para el circuito en equilibrio (250% de carga circulante), procediendo a calcular el valor de Wir (kwh/ton corta) según la fórmula de la ecuación 3 arriba. En dicha expresión, el valor de P100 corresponde a la abertura del tamiz en micrones de la malla de corte seleccionada para cerrar el circuito. - Análisis Granulométrico Completo de la Muestra Test : Se realizará un análisis granulométrico detallado de la muestra test (tamizaje y ciclosizer, hasta aprox. 10 micrómetros), a objeto de determinar su granulometría completa y calcular el tamaño 80% pasante original de dicha muestra (valor de F80t expresado en micrones).
- Preparación del Material de Referencia a la Granulometría Original de la Muestra Test : Con el material de referencia remanente del Test Standard de Bond (unos 10 kg de material ya preparado bajo 6 mallas), se realizarán 4 moliendas de calibración (usando aprox. 1 kg de muestra por test) bajo condiciones pre establecidas, en un molino de bolas rutinario de laboratorio (Ejemplo: D x L = 17 x 22 cm; 70% velocidad critica; 67% sólidos en peso; carga de bolas balanceada prefijada; etc.), determinando la distribución granulométrica del producto molido al término de cada una de estas pruebas. A partir de los resultados granulométricos obtenidos (incluyendo el valor de F30 calculado en el punto 1), se procederá a determinar el valor de P80 (micrómetros) para cada tiempo de molienda (min.). Se graficarán los valores de P80(t) versus t (incluyendo t =0); determinando de dicho gráfico el tiempo de molienda requerido para obtener en la muestra de referencia el mismo valor de F80(micrómetros) previamente calculado en el punto 2, para la muestra test. Empleando el tiempo de molienda seleccionado anteriormente, se realizarán 2 .pruebas de molienda batch con el material de referencia (ej.: mineral de Cu), a objeto de alcanzar la granulometría original de la muestra test (ej.: concentrado de cobre) y' juntar 2 cargas del material de referencia molido, para la posterior ejecución de
pruebas comparativas de molienda con este material y la muestra test. - Determinación del Tiempo de Molienda (o Remolienda) Requerido para la Muestra Test: Se establecerán nuevas condiciones experimentales de molienda (o bien, se mantendrán las del punto 3, dependiendo de cada caso) para moler la muestra test hasta la granulometría final requerida (por ejemplo, si se trata de una muestra de concentrado de Cu que se debe remoler a 90% 325 #, se deberá definir la nueva carga de bolas, % de sólidos, etc., a usar en los test de remolienda de dicho concentrado). Para ello, se harán 4 moliendas de calibración (a distintos tiempos) bajo condiciones experimentales pre establecidas en el molino de bolas de laboratorio, determinan do la distribución granulométrica del producto molido al término de cada una de estas pruebas de calibración. A partir de los resultados granulométricos obtenidos (incluyendo los valores de F80t; y % -325#, determinados en el punto 2), se procederá a calcular los valores de P80 (micrómetros) y % - 325 # (u otra malla de referencia) versus tiempo de molienda (incluyendo resultados para t=0). Se graficarán los valores de % - 325 mallas versus tiempo, determinado de dicho gráfico el tiempo de molienda requerido para obtener la granulometría deseada de la muestra test (ej.:90% -325 # ).Separadamente se graficarán los valores de P80 (t) versus t, determinado de dicho gráfico el valor de P80t que se alcanzaría al término del tiempo de molienda seleccionado para la muestra test.
- Pruebas Comparativas de Molienda : Se harán 2 pruebas comparativas de molienda con la muestra test y el material de
referencia (test en duplicado), a objeto de calcular el valor de Wit. Para ello, se usarán las mismas condiciones operacionales y tiempo de molienda seleccionado en el punto 4, para los dos tipos de muestras, analizando granulométricamente los respectivos productos de molienda, a objeto de determinar los valores de P80 de cada
una de estas muestras (se calculará el valor promedio del P80 de cada muestra, a partir de los respectivos análisis granulométricos efectuados en duplicado), Con los valores de P80,r y P80,t (determinados desde las distribuciones granulométricas de ambos productos molidos) y de los valores de F80,r = F80,t; (calculados de la alimentación a la molienda en ambos casos) y ya conocido el valor de Wi r (punto 1), se procederá a calcular el índice de trabajo de la muestra test (Wi t), utilizando la ecuación 7 para tales efectos.
El método Berry & Bruce modificado por INCO Metals of Canada permite obtener estimaciones bastante confiables (error promedio de ± 5%) del índice de trabajo de una muestra test a partir del Wi conocido de una muestra de referencia, siempre que se sigan correctamente todas las especificaciones entregadas en los puntos 1 a 5 de esta sección. Este método ha sido chequeado experimentalmente para no menos de 50 muestras distintas y variando el tamaño de corte entre 48 # y 270 # Tyler, obteniéndose estimaciones suficientemente precisas para la mayoría de las aplicaciones prácticas.
Etiquetas de Technorati: Wi,indice de trabajo


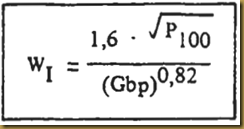




2 comentarios:
Y las fuentes?
Sepulveda CIMM dimensionamiento y optimizacion de plantas metalúrgicas con modelacion matemática
Publicar un comentario